في عالم الرياضيات، يشكّل المثلث واحداً من الأشكال الهندسية الأساسية التي لا غنى عنها في التطبيقات اليومية، من الهندسة المعمارية إلى التصميم الرقمي. وعلى الرغم من بساطة شكله، إلا أن حساب مساحة المثلث يمكن أن يتم بعدة طرق مختلفة، بحسب ما هو متوفر من معطيات. في هذا المقال، نستعرض أشهر هذه الطرق، مع توضيح الحالات التي يُفضّل فيها استخدام كل طريقة، مما يجعل هذا الموضوع مرجعاً مفيداً للطلاب، والمهندسين، والمهتمين بالرياضيات.

أولاً: القاعدة الأساسية

$$\text{المساحة}=\frac{1}{2}\times \text{القاعدة}\times \text{الارتفاع}$$

هذه القاعدة تُعدّ الأكثر شهرة وبساطة. تُستخدم عندما نعلم طول القاعدة وارتفاع المثلث العمودي عليها. يُشترط أن يكون الارتفاع عمودياً على القاعدة، ويُفضَّل استخدام هذه الطريقة عند التعامل مع المثلثات مرسومة بشكل واضح أو عند توفر الرسم البياني.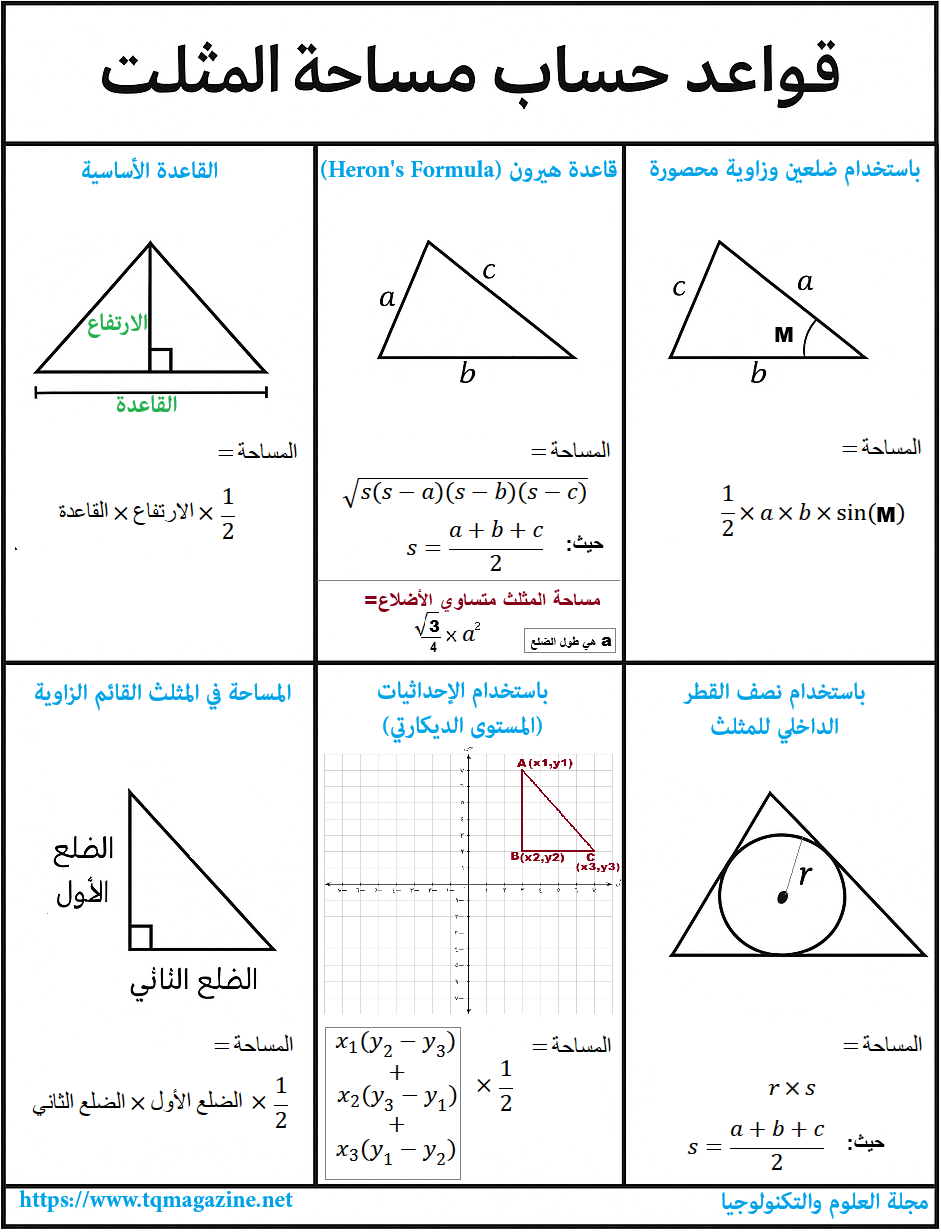 

ثانياً: قاعدة هيرون (Heron's Formula)

$$\text{المساحة}=\sqrt{s(s-a)(s-b)(s-c)}$$

$$s=\frac{a+b+c}{2}$$

هذه القاعدة تناسب المثلثات التي نعرف فيها أطوال الأضلاع الثلاثة فقط، دون معرفة الزوايا أو الارتفاع. وتُستخدم في المسائل التي تتعلق بالمثلثات العشوائية أو غير المنتظمة.

يمكن ان نستنتج منها أو من القاعدة الأساسية مساحة المثلث المتساوي الأضلاع بالمعادلة: 

$$\text{المساحة}=\frac{\mathrm{\surd 3}}{4}\times \mathrm{a²}$$

حيث a هو طول الضلع.

ثالثاً: باستخدام ضلعين وزاوية محصورة

$$\text{المساحة}=\frac{1}{2}\times a\times b\times \sin (C)$$

إذا كانت لدينا زاوية محصورة بين ضلعين معلومين، فإن هذه القاعدة تُعد من أدق الطرق وأسرعها، خصوصاً عندما تكون الزوايا معروفة إما بالراديان أو بالدرجات.

رابعاً: المساحة في المثلث القائم الزاوية

$$\text{المساحة} = \frac{1}{2} \times الضلع الأول \times الضلع الثاني$$المساحة=1/2​×الضلع الأول×الضلع الثاني

في حال كان المثلث قائم الزاوية، فإن القاعدة تختصر الحساب كثيراً، حيث يتم ضرب الضلعين المتعامدين مباشرة دون الحاجة للبحث عن ارتفاع، لأن أحد الضلعين يمثل القاعدة والآخر يمثل الارتفاع.

خامساً: باستخدام الإحداثيات (المستوى الديكارتي)

$$\text{المساحة}=\frac{1}{2}\mid x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)\mid$$

تُستخدم هذه القاعدة عندما تكون رؤوس المثلث معروفة من خلال إحداثياتها في المستوى البياني (س، ص). وتُعد من الأدوات الأساسية في التحليل الهندسي والبرمجة الرسومية.

سادساً: باستخدام نصف القطر الداخلي للمثلث

$$\text{المساحة} = r \times s$$المساحة=r×s

في بعض الأحيان، نعلم طول نصف قطر الدائرة الداخلية للمثلث (الدائرة التي تمس الأضلاع الثلاثة من الداخل). عندها يمكن استخدام هذه القاعدة، حيث

$$s هو نصف محيط المثلث كما في قاعدة هيرون،

$$r هو نصف القطر.

تُستخدم هذه الطريقة في المسائل المتقدمة في الهندسة المستوية والهندسة التحليلية.

خاتمة: الرياضيات في خدمة الإبداع الهندسي

يمنحنا فهم طرق حساب مساحة المثلث مرونة في اختيار الأداة المناسبة لكل حالة، سواء في المسائل المدرسية أو في التطبيقات العملية. فالمثلث ليس مجرد شكل بسيط، بل هو مدخل إلى عالم واسع من الدقة والتفكير المنطقي، حيث تتعدد الطرق والنتيجة واحدة.

⚠️ تذكير:

اختيار الطريقة الأنسب يعتمد على المعطيات المتوفرة: هل نعرف الأضلاع؟ الزوايا؟ الارتفاع؟ أو الإحداثيات؟ عند تحديد هذه العناصر بدقة، يمكن الوصول إلى الناتج بأسرع طريقة وأكثرها دقة.